The complement is a method used to represent the opposite of a positive number in a binary system. It allows for the representation of negative numbers in a way that simplifies arithmetic operations, especially subtraction, which can be converted into addition using the complement. This encoding helps ensure that all numbers within a fixed word length can be represented without ambiguity.
**What does the complement mean?**
In real life, we perform various mathematical operations like addition, subtraction, multiplication, and division. However, computers are built with only one type of circuit: an adder. That means all other operations—like subtraction or multiplication—must ultimately be transformed into additions. So why not design separate circuits for subtraction or multiplication? The answer lies in simplicity. Implementing multiple types of circuits would complicate the design and increase the cost and complexity of the computer. Using only an adder makes the overall system more efficient and easier to build.
Now, let's understand the role of the complement in this context. Computers cannot directly perform subtraction. Instead, they convert subtraction into addition by using the complement of a number. For example, subtracting 5 from 10 is equivalent to adding the complement of 5 to 10. This is how the complement helps in making subtraction easier for the computer.
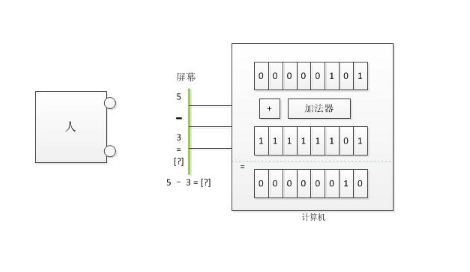
**What is the purpose of the complement?**
- The complement of a positive number is the same as its original form.
- The complement of a negative number is obtained by taking the original code, inverting all the bits (this is called the one’s complement), and then adding 1 to it.
- The sign bit is the leftmost bit, and the rest of the bits represent the magnitude of the number.
- Using complements speeds up calculations because addition is the fastest operation a computer can perform.
- Remember, "code" and "number" are two different things. A number can be represented in many ways, depending on the coding scheme.
When we write numbers, we usually use decimal digits (0–9). But computers store data in binary, which uses only 0s and 1s. The concept of "word length" comes into play here. Word length refers to the number of bits used to represent a number in the computer. Common word lengths include 4-bit, 8-bit, 16-bit, 32-bit, and so on.
Humans tend to think in terms of decimal numbers and often don’t consider word length when writing them. But for a computer, word length defines the size of the numbers it can handle and how it performs operations. This is why the complement is important—it ensures that negative numbers can be represented and processed efficiently.
**Complements in Decimal and Binary**
Just like in binary, complements also exist in decimal systems. To find the complement of a number, you must first define the word length. For instance, in a 4-digit decimal system, the complement of 1234 would be 8766, because 1234 + 8766 = 10000. In this case, 8766 represents -1234.
Similarly, in binary, the complement of a number is calculated based on the total number of bits available. This allows for the representation of negative numbers and makes arithmetic operations more straightforward.
**Who invented the complement?**
Although the exact origin is unclear, the complement was popularized in computing by John von Neumann. Before the complement was widely used, many early computers used the one’s complement, which had some disadvantages. One major issue was the presence of both +0 and -0, which could cause confusion during calculations. The complement eliminates this problem by having only one zero and allowing all operations to be reduced to addition.
**Understanding Complements and Their Logic**
Let’s define a few key concepts:
- For an N-bit binary number, the complement of a number A is given by f(A) = 2^N – A.
- For positive numbers and zero, the original code is the same as the complement.
- For negative numbers, the process involves inverting the bits (one’s complement) and then adding 1.
This method ensures that the complement of a negative number corresponds to the positive value it represents. For example, if A = -1234, then its complement would be 8766 in a 4-digit system.
**Machine Implementation and Practical Use**
On a machine level, the complement allows for efficient computation. When performing subtraction, the computer simply adds the complement of the subtrahend. This reduces the need for separate hardware for subtraction, multiplication, and division.
Another benefit is that the complement simplifies the handling of overflow and underflow. It also ensures consistency in the representation of numbers, making it easier for the computer to process data accurately.
**Reflections on the Idea Behind the Complement**
The invention of the complement was a significant breakthrough in computing. It solved several problems related to the representation of negative numbers and made arithmetic operations more efficient. While there may have been deeper theoretical considerations behind its development, the practical benefits are clear.
From a human perspective, the complement might seem abstract, but from a machine’s point of view, it’s a simple and effective solution. It aligns with the way computers operate, making it an essential part of digital systems.
In summary, the complement is a powerful tool that enables computers to handle negative numbers and perform complex operations efficiently. Its simplicity and effectiveness have made it a cornerstone of modern computing.
Fiber Reinforced Composite Material
Fiber Reinforced Composite Material,Hard Composite Graphite Fiber Felt,Vacuum Furnace Heat Insulation Ring,Insulation Material For Vacuum Furnace
HuNan MTR New Material Technology Co.,Ltd , https://www.hnmtr.com